本記事では、データ分析の基礎になる相関について解説します。データ分析の基礎にあたる知識であり、比較的理解のしやすい概念ではあるものの、落とし穴と呼んでも良い注意点も複数あります。
相関とは?データ分析における基礎知識
相関という言葉は、データ分析を行う上で必ずと言っても良いほど出てくる言葉です。相関を一言で表すと、「あるデータXの変化に対する、別のデータYの変化の傾向」です。数式は以下になります(紹介程度なので、よく分からなくても今は問題ありません)。
#ピアソンの相関係数
r = Σ((Xi - X̄)(Yi - Ȳ)) / √(Σ(Xi - X̄)² * Σ(Yi - Ȳ)²)
r: 相関係数
Σ:総和
Xi, Yi: XとYの各データ点
X̄, Ȳ: XとYの平均重要なのは、相関係数rの値を見てどう解釈するか?です。製造業だと、経験的にrの絶対値が0.6以上なら強めの相関ありと判断することが多いです。
- rは-1~1の間で動く
- rが正のときはXとYは同じ方向(Xが増えたらYも増える)
- rが負のときはXとYは逆方向(Xが増えたらYが減る)
- 絶対値で0.6くらいから強めの相関がある(= 有効そう)と判断
注意すべきは、単純にrの絶対値が0.6以上だからXとYに関係がある、0.6以下だから関係ないとは言えない点にあります。相関の落とし穴と私は呼んでいるので、以下では代表的な3つの落とし穴を紹介します。
【要注意】相関係数の3つの落とし穴
偽相関(疑似相関):データに相関があっても関係がないケース
偽相関(疑似相関)はその名の通りで、ニセモノの相関関係のことを指します。特に初学者は勘違いしがちですが、「相関が強い ≠ 関係がある」です。偽相関の例として、三重大学の奥村名誉教授のホームページで紹介されていたデータを紹介します。
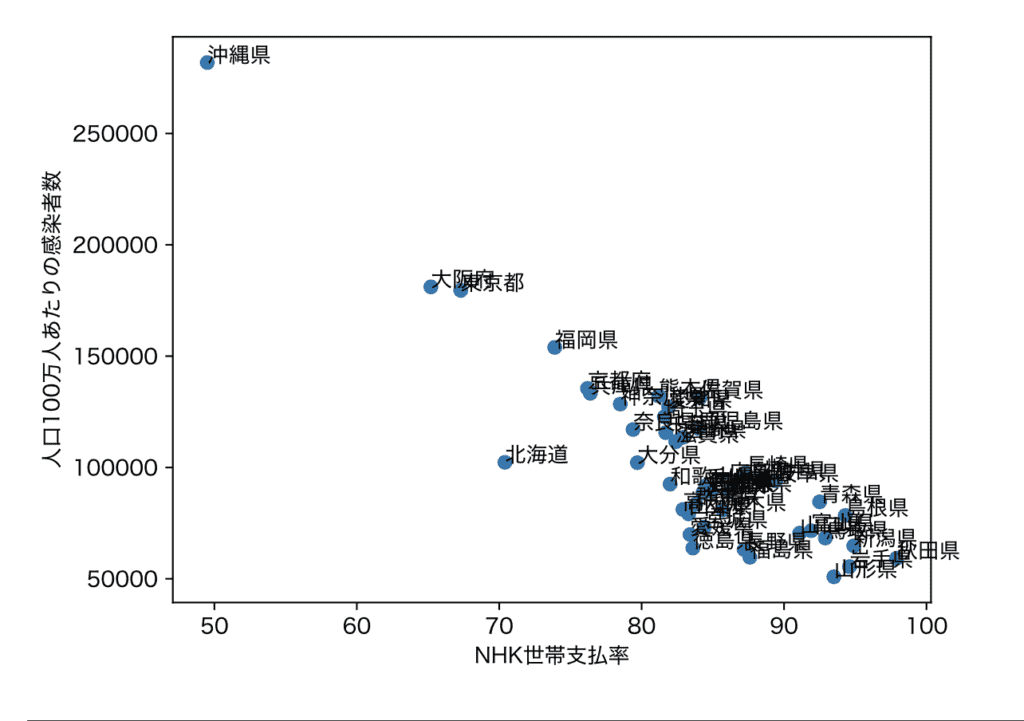
このデータは、r = -0.89で明確な負の相関があります。しかし、「コロナの感染者数とNHK受信料の支払い率に関係がある」と言って良いのでしょうか?確実に無いでしょう。これが偽相関です。全く関係がないデータが、相関係数というレンズを通すと関係あるように見える典型例といえます。
一方で、偽相関だからと言って、すぐに考察をやめるのも勿体ないです。なぜなら、偽相関が見られる別のデータZを見つけるヒントを与えてくれるからです。今回の場合は、「人口の流動性」や「観光などの人の動きの激しさ」が考えられそうす。
p値が不十分:相関係数だけで判断すると失敗する理由
相関係数の高低だけでなく、相関係数を調べたら必ずセットで「p値」についても調べる必要があります。p値を端的に言うと、「今回分析した結果は、全体に対しても同じことが言えるか?」を表しています。詳しい解説は今回の記事の趣旨から外れるため割愛しますが、「p < 0.05ならOK」とまずは覚えてください。
相関が低くても関係があるデータとは?
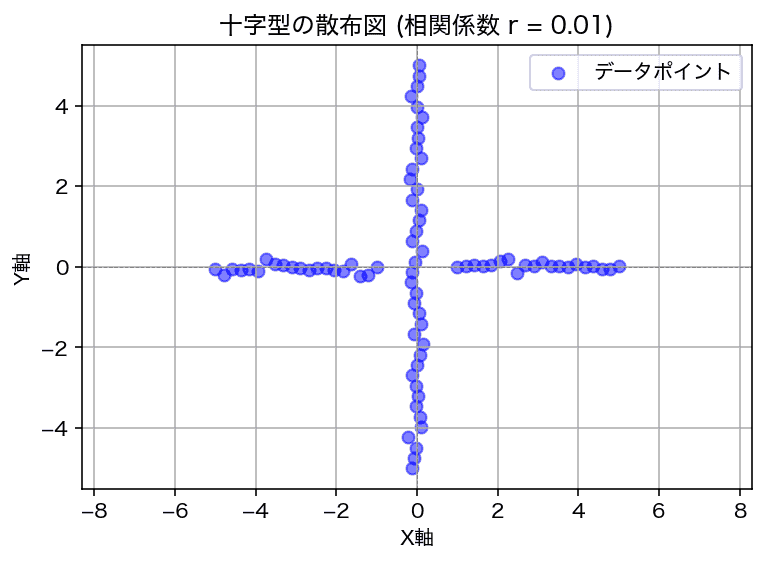
以前の記事でも指摘していますが、相関係数が低くてもデータ間に明確な関係性が存在する場合もあります。例えば、2次関数などの多次元の関係や、図形(円、十字など)を描くような関係にあるときです。下に、相関係数が低いのに明確な関係性がある例として、十字形のプロットを示します。相関係数r = 0.01で極めて低く、これだけ見るとXとYに関係がないと結論付けてしまいますが、実際は明確な関係性が見られます。
このように、データ間に関係があるのに相関が低い理由は、「相関係数はあくまで直線性の関係があるか」を判定しているためです。直線性の関係がないと、相関係数の絶対値は低く見積もられます。
まとめ
以上、今回は相関係数の説明をしました。まとめると
- 相関とは、「あるデータXの変化に対する、別のデータYの変化の傾向」
- 相関係数rは絶対値で0.6以上のとき強い相関があるといえる
- 偽相関は、関係のない2つのデータに相関が見られる現象
- 相関係数だけでなく、p値が0.05未満か見る
- 相関係数が低くても、データ間に関係性がある場合もある
今後、p値の詳しい解説をしたいと思っています。毎週日曜日に更新しているので、ぜひチェックしてください!


コメント