製造に役立つプログラミングの例として、今回は工程能力指数(Cpk)の計算と計算結果を使った抜取検査基準の作り方について解説します。関連記事として、もう一つの工程能力指数Cpについて解説した記事も書きました。こちらもぜひ御覧ください。
抜き取り検査とは?
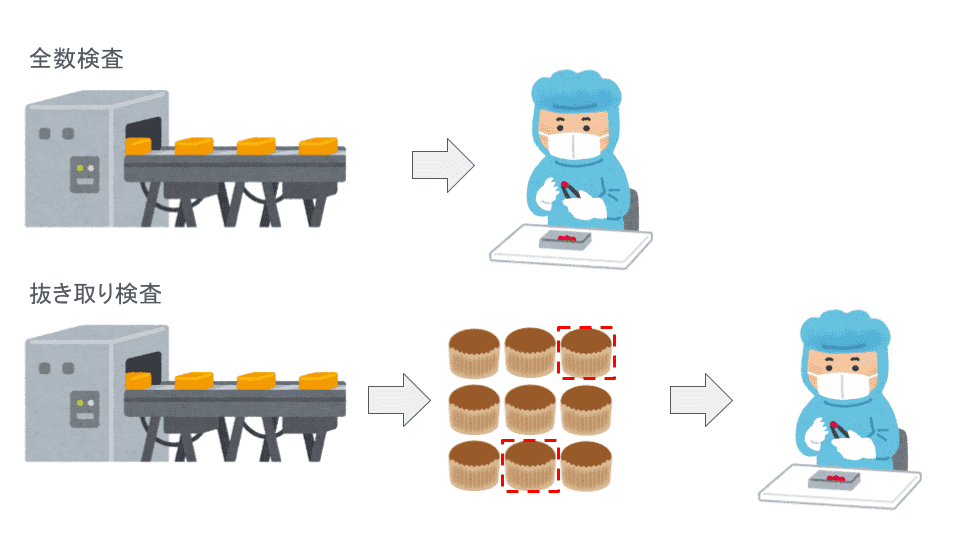
製品の品質を保証するために、製品の特性が基準値を満たしているか評価する必要があります。生産した全ての製品の評価を実施することができれば、不良品を工程内に留め、次工程や顧客への流出を防ぐことができます。しかし、製品の全数検査は現実的には不可能な場合が多いです。そこで、製品を塊(ロット)で管理し、ロット内の一部を評価することで全数検査に替えることを行う場合があります。この評価方法を抜き取り検査といいます。
抜き取り検査を実施するためには、製品の不良発生率を表す、「工程能力(Cpk)」が抜取検査の数や頻度に対して十分であるかを調べる必要があります。
Cpkの計算式とその意味
先ほど、工程能力(Cpk)という言葉が出てきました。Cpkを一言で表すと、「製品特性の上下限値に対する余裕」です。Cpkを式で表すと、以下になります。上限値と下限値、それぞれに対して計算し、小さい方の値をCpkとして採用します。
Cpkが大きいほど、上下限値に対して余裕を持っていて、歩留まりが高く安定した品質を保っている状態であると言えます。式の意味を読み解くなら、「Cpk = 1のときに管理値に対して、製品特性の分布は、6σ(≒ 99.7%)で収まる」ことになります。
Cpk = {x̄-(xmax or xmin)}/3σ
x̄: 任意の製品特性xの平均
xmax: xの管理上限値
xmin: xの管理下限値
σ: xの標準偏差抜き取り基準の設定
Cpkの計算を実施し、抜取検査の基準を設定します。基準は「Cpk ≧ 1.33」です。これはなぜかというと、上記の基準を満たすことができれば、不良発生の可能性が0.006%程度と見積もることができるためです。これは、不良の発生の懸念がほとんどないことを示します。自動車業界は更に厳格に、Cpk ≧ 1.65を求めるケースが多いです。
以下では、仮のデータを使ってCpkの計算や管理値の設定を実践します。今回もPythonを使った計算や描画をコード付きで解説します。必要に応じて、pandasやnumpyをインポートした状態でコードを動かしてください。今回使う仮のデータを以下に示します。
data = {
'日付': [
'2025-01-05', '2025-01-06', '2025-01-07', '2025-01-08', '2025-01-09', '2025-01-10',
'2025-01-11', '2025-01-12', '2025-01-13', '2025-01-14', '2025-01-15', '2025-01-16',
'2025-01-17', '2025-01-18', '2025-01-19', '2025-01-20', '2025-01-21', '2025-01-22',
'2025-01-23', '2025-01-24', '2025-01-25', '2025-01-26', '2025-01-27', '2025-01-28',
'2025-01-29', '2025-01-30', '2025-01-31',
'2025-02-01', '2025-02-02', '2025-02-03', '2025-02-04', '2025-02-05', '2025-02-06',
'2025-02-07', '2025-02-08', '2025-02-09', '2025-02-10', '2025-02-11', '2025-02-12',
'2025-02-13', '2025-02-14', '2025-02-15', '2025-02-16', '2025-02-17', '2025-02-18',
'2025-02-19', '2025-02-20', '2025-02-21', '2025-02-22', '2025-02-23', '2025-02-24',
'2025-02-25', '2025-02-26', '2025-02-27', '2025-02-28',
'2025-03-01', '2025-03-02', '2025-03-03', '2025-03-04', '2025-03-05', '2025-03-06',
'2025-03-07', '2025-03-08', '2025-03-09', '2025-03-10', '2025-03-11', '2025-03-12',
'2025-03-13', '2025-03-14', '2025-03-15', '2025-03-16', '2025-03-17', '2025-03-18',
'2025-03-19', '2025-03-20', '2025-03-21', '2025-03-22', '2025-03-23', '2025-03-24',
'2025-03-25', '2025-03-26', '2025-03-27', '2025-03-28', '2025-03-29', '2025-03-30',
'2025-03-31'
],
'ロットID': [
'L001', 'L002', 'L003', 'L004', 'L005', 'L006', 'L007', 'L008', 'L009', 'L010',
'L011', 'L012', 'L013', 'L014', 'L015', 'L016', 'L017', 'L018', 'L019', 'L020',
'L021', 'L022', 'L023', 'L024', 'L025', 'L026', 'L027', 'L028', 'L029', 'L030',
'L031', 'L032', 'L033', 'L034', 'L035', 'L036', 'L037', 'L038', 'L039', 'L040',
'L041', 'L042', 'L043', 'L044', 'L045', 'L046', 'L047', 'L048', 'L049', 'L050',
'L051', 'L052', 'L053', 'L054', 'L055', 'L056', 'L057', 'L058', 'L059', 'L060',
'L061', 'L062', 'L063', 'L064', 'L065', 'L066', 'L067', 'L068', 'L069', 'L070',
'L071', 'L072', 'L073', 'L074', 'L075', 'L076', 'L077', 'L078', 'L079', 'L080',
'L081', 'L082', 'L083', 'L084', 'L085', 'L086'
],
'ロットサイズ': [1000] * 86,
'規格上限値': [20.05] * 86,
'規格下限値': [19.95] * 86,
'特性値': [
20.01, 20.00, 20.00, 19.99, 20.00, 20.01, 20.00, 19.98, 19.99, 20.00,
20.01, 20.00, 19.99, 20.02, 20.03, 20.02, 20.02, 20.01, 20.00, 19.97,
19.96, 19.97, 19.98, 19.99, 20.00, 20.01, 20.00, 19.99, 20.00, 19.99,
19.99, 19.98, 19.99, 20.00, 20.01, 20.00, 19.99, 20.00, 20.01, 20.00,
20.00, 20.01, 20.01, 20.00, 19.99, 20.00, 20.01, 19.97, 19.99, 20.01,
20.00, 19.99, 20.00, 20.01, 20.00, 19.99, 20.00, 20.01, 20.00, 19.99,
20.00, 20.01, 19.98, 20.00, 20.00, 19.99, 20.00, 20.01, 20.00, 19.99,
20.00, 20.01, 20.00, 19.99, 20.00, 20.01, 20.00, 19.99, 20.00, 20.01,
20.00, 19.99, 20.00, 20.01, 20.00, 19.99
]
}
# Pandasデータフレームに変換
df_inspection = pd.DataFrame(data)平均値やσ、工程能力の計算
まずは平均値の計算から行います。
average_value = df_inspection['特性値'].mean()
#必要に応じて表示する。
print(f'特性値の平均値: {average_value:.4f}')次に、σの計算を行います。
# σ(=不偏標準偏差)の計算
sigma = df_inspection['特性値'].std(ddof=1)
#必要に応じて表示する。
print(f'特性値の標準偏差 (σ): {sigma:.4f}')平均とσの計算ができたため、Cpkの計算を行います。
# 規格上限値 (Upper Specification Limit)
usl = df_inspection['規格上限値'].iloc[0]
# 規格下限値 (Lower Specification Limit)
lsl = df_inspection['規格下限値'].iloc[0]
Cpk = min((usl - average_value) / (3 * sigma), (average_value - lsl) / (3 * sigma))
print(f'工程能力指数 Cpk: {Cpk:.4f}')以上を計算した結果が以下になります。Cpk > 1.33で、高い工程能力を持っていることがわかり、抜き取り検査を実施しても良いと判断できます。
特性値の標準偏差 (σ): 0.0117
平均値: 19.9985
工程能力指数 Cpk: 1.3774
工程能力と標準偏差(σ)に基づく管理値の設定
Cpkの計算を実施し、抜取検査を実施可能な工程能力を持つことを示すことができました。今度は実際に抜き取り検査を実施するため、管理値を設定します。
設定した管理値内に抜き取り検査の結果が収まるなら、生産条件を変えずに抜き取り検査を継続、管理値から外れた場合は生産条件を調整し、調整後の検査でも管理値から外れるようなら工程に異常が生じていると判断します。
管理値の設定方法はシンプルで、上下限値の中央に対し、上と下それぞれにぶれた場合にCpk ≧ 1.33を保つことのできる範囲とします。今回の場合は、20.00±0.006となり、かなり厳しい管理値が設定されます。
トレンドラインの描画と分析
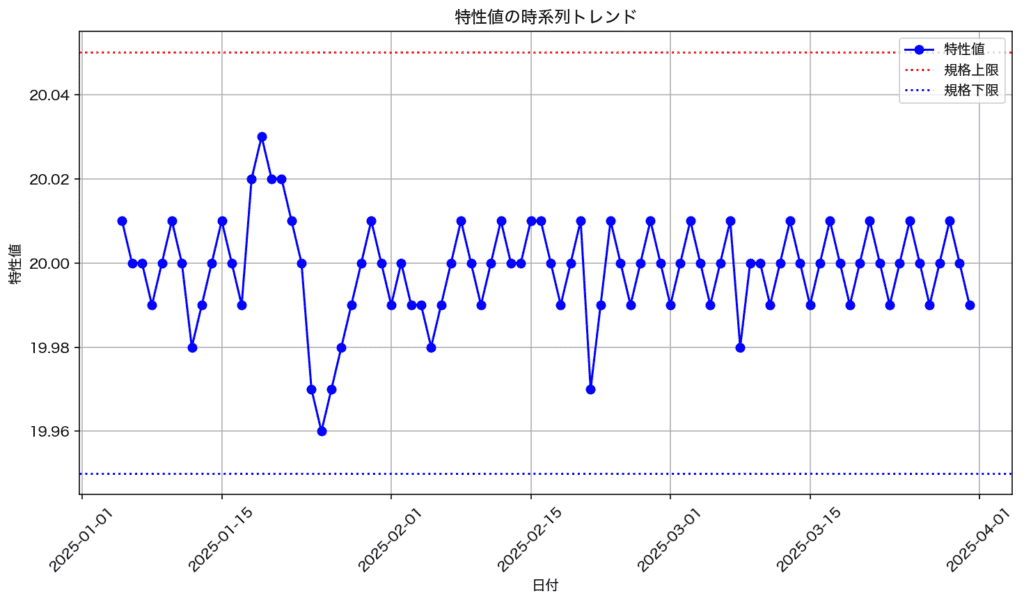
最後に、抜き取り検査頻度を設定します。頻度はトレンドラインを見て判断することもあります。トレンドラインというのは、日ごとの評価結果の変動のことを指します。今回のデータを使ってトレンドラインを描画するには、以下のコードを用います。必要に応じてmatplotlibをインポートしてください。コードを実行した結果を眺めると、初期に大きな変動が起きており、だいたい4ロットごとに評価を実施することで特性の波を捉えられると判断できます。したがって、今回の抜き取り検査は4ロットごととして実行することにします。
# プロット
plt.figure(figsize=(12, 6))
plt.plot(df_inspection['日付'], df_inspection['特性値'], marker='o', linestyle='-', color='blue', label='特性値')
# 規格上限・下限ライン
plt.axhline(y=df_inspection['規格上限値'].iloc[0], color='r', linestyle=':', label='規格上限')
plt.axhline(y=df_inspection['規格下限値'].iloc[0], color='b', linestyle=':', label='規格下限')
# グラフの設定
plt.xlabel('日付')
plt.ylabel('特性値')
plt.title('特性値の時系列トレンド')
plt.xticks(rotation=45)
plt.legend()
# 表示
plt.show()まとめ
今回は、工程能力に関する解説とその値を使った抜き取り検査の方法について解説をしました。今後も製造業の役に立つ統計の知識やプログラミングについて精力的に発信したいと思っています。参考にして頂ければ幸いです!


コメント