初心者向け】統計的仮説検定の基礎をわかりやすく解説

昨今のデータサイエンスやAIの隆盛は皆さん周知の事実だと思います。一方で、これらの発展のバックグラウンドが統計学にあることはあまり意識されていません。今回の記事では、統計分析の基礎になる、統計的仮説検定について初学者向けに解説しました。仮説検定を覚えておくと、工場で起こった品質や装置に異常の疑惑が生じたときに判定ができるようになるため、非常に便利です。

なお、今回の記事は以下のサイトを参考にしています。いずれも優れた内容ですが、一部初学者が混乱しそうな内容や、詳しすぎるように思える部分があったため、今回の解説記事を書きました。

統計的推定と統計的仮説検定

総務省統計局、統計研究研修所の共同運営によるサイトです。国勢の基本に関する統計の企画・作成・提供、国及び地方公共団体の統計職員に専門的な研修を行っています。

23-5. 検定統計量と棄却域・採択域 - 統計WEB

■検定統計量身長や体重などについて検定を行う場合は、コインの裏表が出る確率とは異なり、取りうる値がどのくらいの確率でその値となるかが分かりません。そこで、身長や体重の値を「検定するための値」に変換します。このようにして … 続きを読む 2...

シナリオで学ぶ仮説的統計検定
1. 統計的仮説検定とは？基本の概要
2. 仮説検定の流れ：シナリオで学ぶ
まとめ

シナリオで学ぶ仮説的統計検定

統計的仮説検定とは？基本の概要

統計的仮説検定を平たく言うと、「採用したい仮説Aと、仮説Aに背反な仮説Bを設定し、確率的に仮説Bが成り立たないことを証明することで、仮説Aが正しいと主張する」手法です。文章だけだと分かりづらいと思うので、架空のお菓子工場Xで生産した菓子の重量の異常を題材に仮説検定の流れを説明したいと思います。下に、今回実施する仮説検定のシナリオを示します。

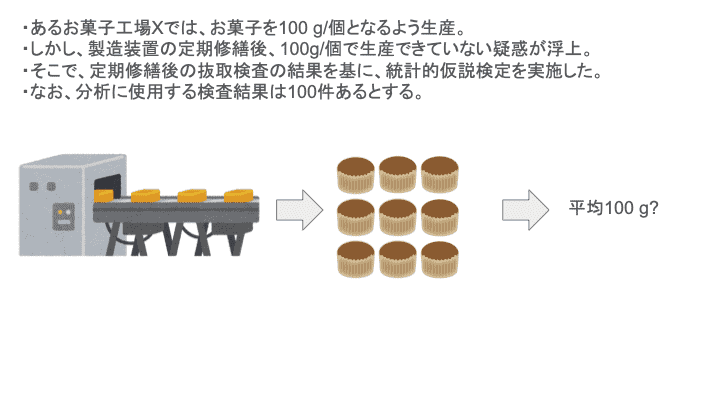
仮説検定の流れ：シナリオで学ぶ

統計的仮説検定は以下の流れで進めます。

帰無仮説と対立仮説の設定
帰無仮説に対して仮説検定を実施
帰無仮説が棄却できれば対立仮説を採用

聞き慣れない言葉が多いと思うので、以下で用語を含め解説します。

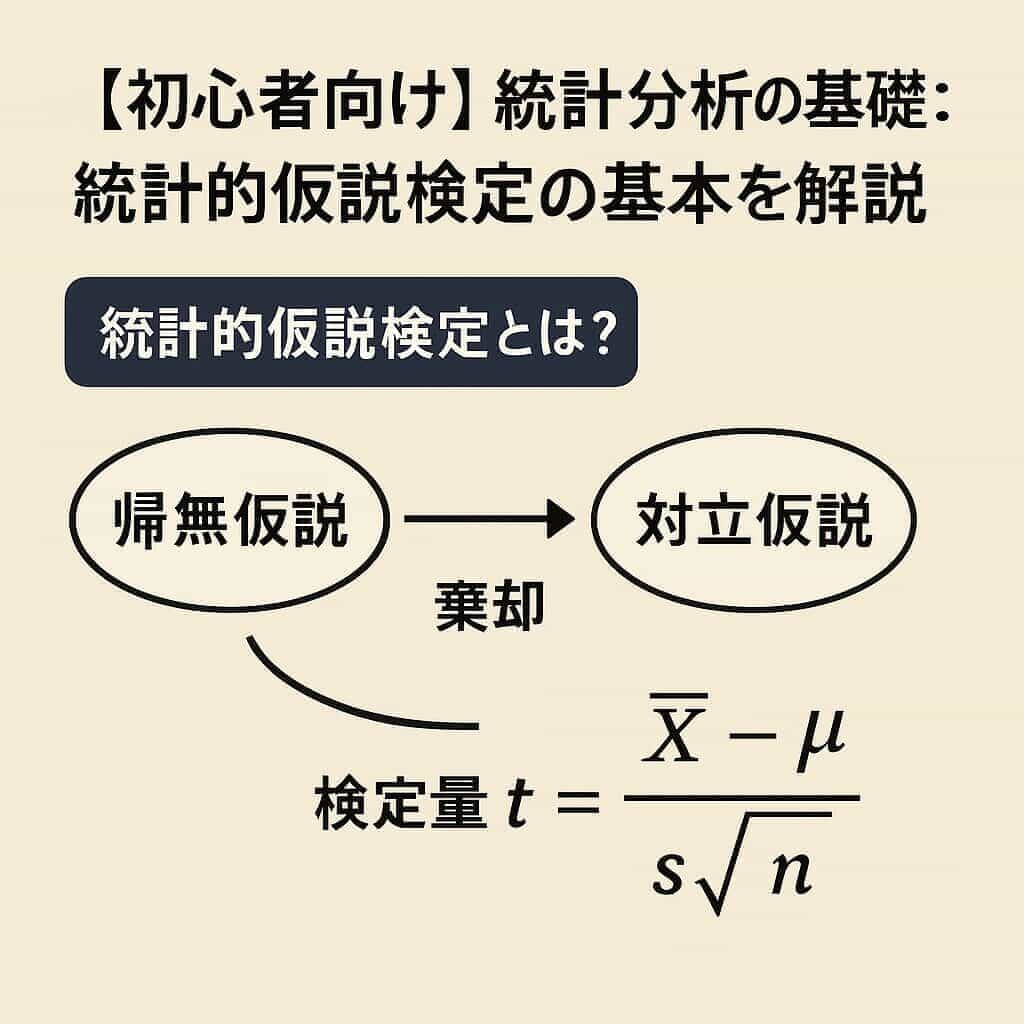
1. 帰無仮説と対立仮説の設定

説明がややこしくなるため、対立仮説から説明をします。対立仮説は、「証明したいと思っていること」です。一方、帰無仮説は、「否定できれば対立仮説(=証明したいこと)が正しいと示せること」です。よって、今回のシナリオでは、

対立仮説 = 「お菓子の重量の平均が100 g/個ではない」
(対立仮説の反証として)帰無仮説 = 「お菓子の重量の平均が100 g/個である」

「帰無仮説を否定することで、対立仮説(本当に立証したいこと)を証明する」のが仮説的統計検定の肝になります。

(補足): 帰無仮説が否定できなかった場合は、帰無仮説が成立することを意味するわけではないことに注意が必要。

2. 帰無仮説に対する仮説検定の実施

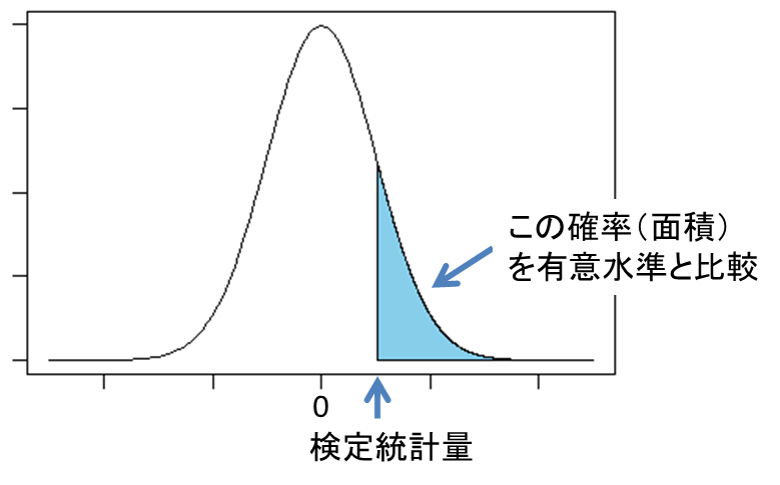
帰無仮説と対立仮説が設定できたら、次は帰無仮説に対して仮説検定を実施します。仮説検定は、「設定した有意水準(=仮説が正しいかを判定する基準)を満たすか否か」で判断します。多くの場合は、有意水準を0.05に設定します。設定した有意水準0.05を下回れば、帰無仮説が正しくないと判断し、対立仮説が正しいと判定します。

有意水準0.05の意味は、「帰無仮説が正しいとして、今回観測した結果が起こる確率が5%かどうか」です。有意水準を下回れば、帰無仮説がほんとに正しいなら、観察された結果(今回なら、抜き取り検査100件の平均値)が起こる確率は5%未満である、ということになります。5%未満の確率で起こる現象が見られることは、ほとんどありえないと判断できるため、帰無仮説が正しくないと判断できるのです。

今回のシナリオでは、「作っているお菓子全体の平均重量が100 gである」確率を、抜き取り検査の結果100件を基に、いわゆる「t検定」という手法で計算します。式を以下に示します。

検定量t = (X̄ - μ) / (s /√n)

X̄:サンプルの平均(標本平均)
μ:母集団全体の平均(母平均)
s:サンプルの標準偏差(不偏標準偏差)
n:サンプル数(今回は100)

なお、不偏標準偏差の計算式は以下になります。不偏標準偏差は、「サンプルの測定結果から計算した、母集団のばらつきの幅」のことを指します。今回は詳細を省きます。

s = √( Σ (Xᵢ - X̄)² / (n - 1) )
Xᵢ:各サンプルの測定値(今回なら、各抜き取り検査の重量)

「母集団の平均」という言葉が聞き慣れないと思うので補足します。母集団と言うのは、今回なら「定期修繕後に作った全てのお菓子」のことになります。帰無仮説を検定する都合上、今回は母平均μ = 100として検定量tを計算します。

3. 帰無仮説の棄却と対立仮説の採用

tの値が0.05を下回れば、「生産したお菓子全体の平均が100 g/個である可能性は5%未満である」ことになり、確率的にありえないと判断します。「ありえないと判断すること」を一般的に棄却と言い、帰無仮説を棄却できれば対立仮説が正しいと判断する(採用する)ことになります。

ここで、tが0.05を上回った場合を考えます。このとき、帰無仮説を棄却できません。では、棄却できないなら、帰無仮説は正しいと言えるのでしょうか？答えは、「帰無仮説を棄却できないからと言って、正しいことにはならない」です。この点は非常に注意が必要になります。

まとめ

今回は、統計分析の基礎になる仮説的統計検定について解説しました。仮説的統計検定は、

帰無仮説と対立仮説を設定し
帰無仮説を検定して
帰無仮説を棄却することで、対立仮説を採用する

ことが、一般的な流れになります。また、帰無仮説を検定した結果、棄却できなかった場合は帰無仮説が正しいことにはならない点も重要であると言えます。次回以降は、よりモノづくりの現場で実際に役立つ統計知識についても発信したいと思います！

【初心者向け】統計的仮説検定の基礎をわかりやすく解説